可评估性（与假期购物省钱技巧）

原文：Evaluability (and Cheap Holiday Shopping)

随着「万圣感恩圣诞」季最烧钱的阶段日渐临近，一个问题想必正萦绕在我们读者的心头：

「亲爱的 Overcoming Bias，有没有什么偏见可供我利用，好让我显得很大方，又不用真的花太多钱呢？」

我很高兴地告诉大家，答案是肯定的！Hsee 在一篇题为 Less is better: When low-value options are valued more highly than high-value options 的论文中指出：给别人送一条价值 45 美元的围巾，会比送一件价值 55 美元的外套，更有可能让别人觉得你很慷慨。[1]

这其实是一种更普遍现象下的特例。在早前的一项实验中，Hsee 曾让受试者为二手音乐词典估价：[2]

• 词典 A：1993 年出版，收录 1 万词条，品相如新。

• 词典 B：1993 年出版，收录 2 万词条，封面有破损，其余部分品相如新。

这个实验的巧妙之处在于：一部分受试者可以同时看到两本词典并进行比较评估，而另一部分受试者则只能看到一本……

那些只能看到其中一本词典的受试者，对词典 A 的平均出价为 24 美元，对词典 B 则为 20 美元。而可以同时看到两本词典的受试者，他们愿意为词典 B 出价 27 美元，为词典 A 出价 19 美元。

当然，词典的收词量要比封面破不破损重要得多，至少在你真要用它的情况下是这样的。但如果摆在你面前的只有一本收录了两万词条的词典，那么「两万」这个数本身其实并不能说明太多问题——这个数算多还是少？谁知道呢？它是无法评估的。而另一方面，封面破损的问题就显得尤为突出，因为它带有明确的情感效价——负面的那种。

但当两本词典并列摆放时，词条数量就从不可评估变得可以评估了，因为此时有了两个可以进行比较的同类数据。而且，词条数量一旦变得可评估，其重要性就会完全压倒封面破损的瑕疵。

来自 Slovic 等人的研究：你会选哪个？[3]

1. 有 29/36 的概率赢 2 美元。

2. 有 7/36 的概率赢 9 美元。

尽管这两个选项的平均估价（等价货币价值）分别为 1.25 美元和 2.11 美元，但平均吸引力评分却分别是 13.2 和 7.5。此处的价格和吸引力评分是在这样的情境下得出的：受试者被告知，实验将从已评估的赌局选项中随机抽取两个，而他们会参与的是其中估价更高或吸引力评分更高的那个。（因此，受试者有动机为他们自己真正想玩的赌局给出更高的估价或吸引力评分。）

估价更高的赌局反而显得没那么吸引人，这是经典的「偏好逆转」现象。研究人员推测，获胜金额与「定价」任务更契合，而获胜概率则与评估「吸引力」更契合。于是（研究人员心想），何不设法让赌局的收益在情感上更突出——在感受上更可评估——从而更有吸引力呢？

那他们是怎么做到的呢？方法是在赌局中加入一个微不足道的损失。原来的赌局有 7/36 的概率赢 9 美元；新的赌局也有 7/36 的概率赢 9 美元，但同时还有 29/36 的概率输 5 美分。在原来的赌局中，你自然会去评估 9 美元的吸引力。而新的赌局则在引导你去评估赢 9 美元相对于输 5 美分的吸引力。

Slovic 等人表示：「结果超乎我们的预料。」在新的实验中，那个只赢不输的简单赌局，其平均吸引力评分为 9.4；而那个加入了输钱机制的复杂赌局，其平均吸引力评分却高达 14.9。

一项后续实验测试了受试者在「原来的赌局」和「确定能获得 2 美元」之间更愿意选哪个。结果，只有 33% 的学生选择了原来的赌局。而在另一组需要在「确定的 2 美元」和「新赌局」（即增加了输 5 美分可能性的那个）之间选择的受试者中，竟然有高达 60.8% 的人选择赌一把。说到底，9 美元本身算不上一笔多吸引人的钱，但 9 美元对 5 美分的盈亏比，却有着惊人的吸引力。

添加一个纯粹的损失，反而能让赌局更有吸引力！心理学是不是很有意思？这也就是为什么，任何一个真正懂得欣赏人类智能精妙复杂性的人，都不会想要去设计类人人工智能。

当然，这套把戏只有在受试者无法将两个赌局并列比较时才奏效。

类似地，在 Hsee 1998 年的一项研究中，你认为受试者更喜欢下面哪一款冰淇淋呢？

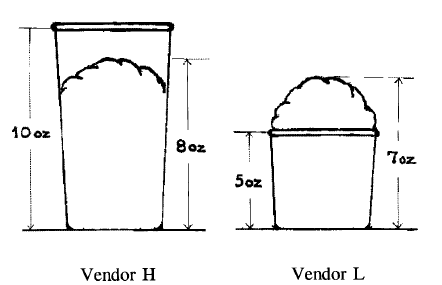
图片来源：Hsee, © 1998 John Wiley & Sons, Ltd.

你可能已经猜到了，答案取决于受试者是只看到其中一款冰淇淋，还是将两款并列比较。当受试者只能看到一款冰淇淋时，他们愿意向商家 H 支付 1.66 美元，向商家 L 支付 2.26 美元。而当他们同时看到两款冰淇淋时，他们愿意向商家 H 支付 1.85 美元，向商家 L 支付 1.56 美元。

这对你的节日购物有何启发呢？是这样的：花 400 美元买一个 16GB 的 iPod Touch，你的收礼人看到的是一部最高端的 MP3 播放器；而花同样的 400 美元买一台任天堂 Wii，他看到的则是一台最入门级的游戏机。哪个性价比更高呢？啊，但这个问题只有在你将两者并列比较时才有意义。你在购物时会把它们放在一起权衡，但收礼人只看得见自己收到的那件礼物。

如果你的预算是固定的——并且你的目标是彰显情谊，而非真正地帮助对方——那么刻意不去追求性价比，效果反而会更好。你先想好要花多少钱来打动对方，然后就用这笔钱，去买一件最不实用的东西。因为在预算固定的前提下，物品的品类越是廉价，你送的这件特定物品就会显得越是昂贵。想一想，一件 25 美元的衬衫和一支 25 美元的蜡烛，哪个更令人印象深刻？

这可真是赋予了日本人购买 50 美元天价甜瓜的习俗一番全新的含义，不是吗？每当看到这种事，你或许会摇着头感叹：「日本人到底是怎么回事？」然而，他们仅仅花了 50 美元，就营造出了一种极其慷慨、甚至挥金如土的形象。你花 200 美元吃一顿豪华大餐，所彰显的阔绰程度，可能还不如花 50 美元买一个甜瓜来得有效。要是社会上能有送 25 美元的牙签或 10 美元的灰尘的习俗就好了；那样他们还能花得更少。

附言：如果你真的用了这一招，请务必告诉我你买了什么。